Stepper FOC Controller Simulation

回顾： 在无刷电机的FOC控制里，其核心思想是"解耦"，利用数学中的坐标变换，将三相坐标系下电机电流转换到交轴Iq与直轴Id,再通过设计控制器如PID,ADRC等方法对电机完成控制。而步进电机，其本质也可以理解为一种两相的无刷电机，因此，可以借鉴三相无刷电机的FOC控制，实现步进电机的精准控制。

步进电机模型

对于常见的步进电机控制方法，也就是脉冲控制，指的是输入一个脉冲，电机转子就步进一下，所以在这种控制方法下，输出的角度和脉冲数有关，成正比，而转速则和脉冲的频率有关。对于此次使用的两相四线步进电机，有四根线，电机可以简化成一下模型：

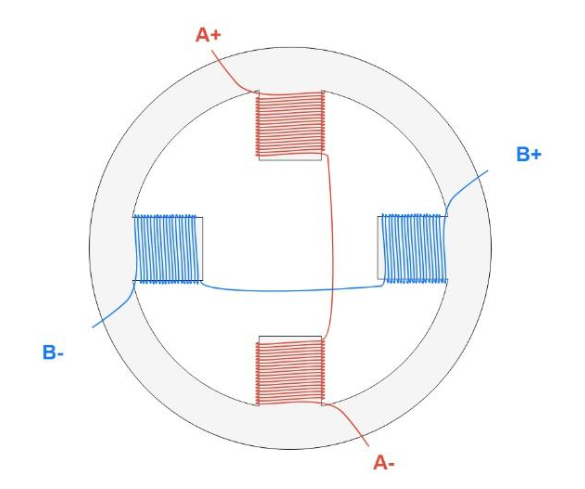
通俗来理解，就是当电流从A+流入，A-流出时，产生了一个N-S磁极，吸引中间的转子转动，接着换B+流入B-流出，产生另一对磁极，不断吸引转子转动。而在此过程中，衍生出很多控制方式，对于现在成本较高的，也就是混合式步进电机，大概是这样：

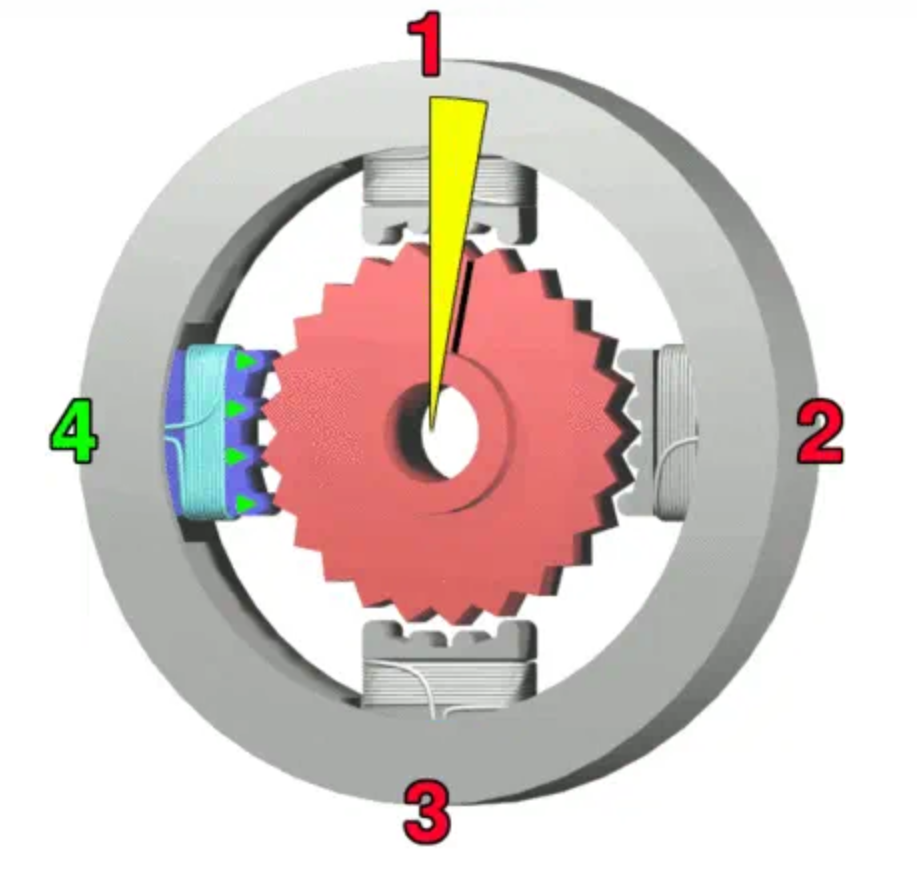
转子是带齿冠的，因此分辨率更高，通常都是1.8°的步距角，也就是转一圈200个脉冲。我们要控制的也是这种电机。

foc控制

clark变换

经过BLDC的FOC控制，可以知道核心的一部分就是通过坐标变换，也就是先使用clark变换将三个相位相差120°的正弦信号转换到α-β两相坐标系下，这一步也很简单，就是：

$$\left \{\begin{aligned}I_{\beta} &= \sin\frac{2\pi}{3} I_{b} - \sin\frac{2\pi}{3} I_{c} \\I_{\alpha} &= I_{a} + \cos\frac{2\pi}{3} I_{b} + \cos\frac{2\pi}{3} I_{c}\end{aligned}\right.$$

而我们的步进本身就是两相直角坐标系，因此，反而是省去了clark变换这一步。

park变换

对于park变化，和bldc时一致，也就是把两相静止的α-β坐标转换到随转子θ旋转的qd轴上，也是比较简单的数学变换：

$$\left \{\begin{aligned}I_{d} &= \cos(\theta) I_{\alpha } + \sin(\theta) I_{\beta} \\I_{q} &= -\sin(\theta) I_{\alpha } + \cos(\theta) I_{\beta}\end{aligned}\right.$$

SVPWM

除了基础的数学变换,另一个关键的部分就是SVPWM的计算过程,这一块需要和BLDC的SVPWM计算过程调整一下。 由于步进电机两个线圈之间没有连接,因此需要两个H桥来控制AB相,先画出逆变示意图:

如果我们记:

$$S_{x} = \left \{\begin{aligned}1-上桥臂连通，下桥臂断开 \\0-上桥臂断开，下桥臂连通\end{aligned}\right.$$

对于BLDC的三相全桥逆变,一共有$2^{3}$个基础矢量，而步进这里有四个全桥，也就是有$2^{4}$个基础矢量，

以一种情况为例:如A+的上桥臂连通,下桥臂断开,A-、B+、B-相的上桥臂断开，下桥臂断开，此时，也就是$S_{a+} = 1,S_{a-} = 0,S_{b+} =0,S_{b-} = 0$, 此时$U_{A+} = U_{dc}$,以此类推，得到：

$S_{a+}$	$S_{a-}$	$S_{b+}$	$S_{b-}$	$U_{\alpha}$	$U_{\beta}$	模长
0	0	0	0	0	0	0
0	0	0	1	0	-$U_{dc}$	$U_{dc}$
0	0	1	0	0	$U_{dc}$	$U_{dc}$
0	1	0	0	-$U_{dc}$	0	$U_{dc}$
0	0	1	1	0	0	0
0	1	0	1	-$U_{dc}$	-$U_{dc}$	$\sqrt{2}U_{dc}$
0	1	1	1	-$U_{dc}$	0	$U_{dc}$
0	1	1	0	-$U_{dc}$	$U_{dc}$	$\sqrt{2}U_{dc}$
1	0	0	0	$U_{dc}$	0	0
1	1	0	0	0	0	0
1	0	1	0	$U_{dc}$	$U_{dc}$	$\sqrt{2}U_{dc}$
1	0	0	1	$U_{dc}$	-$U_{dc}$	$\sqrt{2}U_{dc}$
1	0	1	1	$U_{dc}$	0	$U_{dc}$
1	1	1	0	0	$U_{dc}$	$U_{dc}$
1	1	0	1	0	-$U_{dc}$	$U_{dc}$
1	1	1	1	0	0	0

并画出16个矢量的矢量圆图：

最终将矢量圆分为了四个扇区：

以扇区1为例：

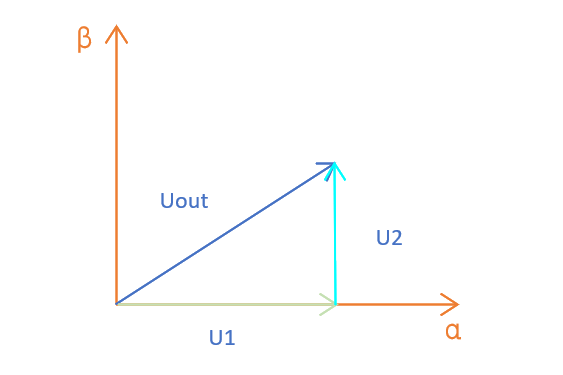
记T为总时长，$T_{0}$为零矢量时间，$T_{1}$为在α轴上($U_{0}$)上的作用时间，$T_{2}$为在β轴上($U_{90}$)上的作用时间，所以

$T = T_{0} + T_{1} + T_{2}$
$U_{2} = (T_{2}/T) U_{90}$
$U_{1} = (T_{1}/T) U_{90}$ 也就是：

$$\left \{\begin{aligned}U_{\alpha} &= \frac{T_{1}}{T}|U_{0}| \\U_{\beta} &= \frac{T_{2}}{T}|U_{90}|\end{aligned}\right.$$

同时为了保证幅值不变原则，需要使$|U_{0}| = |U_{90}| = \sqrt{2}U_{dc}$

因此，容易得出四个扇区各个矢量占空比关系：

扇区	I	II	III	IV
$T_{b}$	$\frac{\sqrt{2}}{2}U_{\beta}$	$\frac{\sqrt{2}}{2}U_{\beta}$	-$\frac{\sqrt{2}}{2}U_{\beta}$	-$\frac{\sqrt{2}}{2}U_{\beta}$
$T_{a}$	$\frac{\sqrt{2}}{2}U_{\alpha}$	-$\frac{\sqrt{2}}{2}U_{\alpha}$	-$\frac{\sqrt{2}}{2}U_{\alpha}$	$\frac{\sqrt{2}}{2}U_{\alpha}$

使用N=2*b+a+1来计算扇区:

扇区	b	a	N
1	1	1	4
2	1	0	3
3	0	0	1
4	0	1	2

Simulation

所以大致思路就是对电机获得的αβ电流以及转子θ角度，park变换得到dq电流，对dq电流进行控制，将输出的dq电压进行反park变换,得到应输出的αβ电压，送入svpwm计算，最终给硬件全桥，来控制电机。接下来就来搭建simulation过程，使用matlab的simulink工具